I felt lucky then and I feel lucky about the same thing now. That first time, it was because the maths teacher stood in front of the class and said ‘You are lucky.’ I was the kind of kid who didn’t question the wisdom of teachers; if he was saying it, it must be true. Apparently, ours was the first year in my school to be taught New Maths by enthusiastic teachers using the SMP books.
I took to New Maths like a duck to water. Up to then, I hadn’t been much use at arithmetic, so it was like a fresh breeze to learn about the way that numbers interacted from this whole new perspective: the development of numerical literacy through exploration and understanding. From illustrations in the real world grew logical constructions. From that core, sprouted and blossomed concepts like geometry and algebra and graphs and calculus. Formulas in this environment were a notation for understanding, rather than something to be learnt for their own sake. Maths, and the world described by maths became an Alladin’s cave. Infinite treasured tunnels fortuitously joined up again around the corner in an intricate network; there for the exploration.
There was a backlash a few years later, especially in the US, where in 1999, according to Wikipedia, Time Magazine placed New Maths on a list of the 100 worst ideas of the 20th century. So I am doubly lucky. I developed a lifelong love of a subject, and my timing was fortuitous. Had I been born a year earlier or a few years later, I could have learnt to hate it and life would have been greyer.
I should be grateful to the culture of my school perhaps, because I think this exploratory teaching spilled over into Physics – (though it certainly never made it across the corridor to Chemistry and Biology, which is a pity.) I remember that in the chapter on Topology, the New Maths book reproduced some illustrations of bones from different species of animals, showing how their structure was essentially the same, but stretched a bit here, compressed there, depending on the structural requirements of the animal’s size and lifestyle. These illustrations were captioned as coming from a source that I made a note of, and a few years later as an Architecture undergraduate, I chanced upon the book in the union bookshop. It went by the catchy handle of On Growth and Form by D’Arcy Wentworth Thompson, abridged by J T Bonner. The book blew my mind, but not because of the idea that related animals have forms mutually stretched about by overlaying and distorting cartesian grids. It was the structures of the tiniest invertebrates that did that for me.
Thompson showed that the growth of these molluscs and sponges takes place because the organism works with the laws of physics to lay down material in places that suit it. To put that another way, these little skeletons are the shape that they are, not because of their form following the necessities of evolution, but because of the physics that govern their construction. The two images I recall after almost half a century are drawings of shells and spicules.
Many types of molluscs grow by a process where material is laid down on the edge of a doubly curved shell. Because the material is added to the edge of a curved shape, the added layer is a tiny bit bigger each time, and so you get a shape that grows in an exactly self-similar expanding geometry . The obvious case is the logarithmic spiral of a snail shell or a cockle, but actually lots of seashells are constructed the same way, even non spiral ones. I still wonder when I pick up a scallop on the sand how perfectly the little tiny shell of the baby scallop is still visible there.

The other picture was of spicules. These little spiky shapes are the skeletal structures of sponges and I recall that Thompson suggested that that the common tetrahedral shape is physically formed by material being precipitated at the junctions of bubbles in foam. I don’t really care whether I got that right or I am inventing the memory, it still shocked me and exploded in my head. Maybe I should check that book lying in my attic but I really don’t want to, the idea is so beautiful.
Look at road junctions in the countryside. Not in the city so much. In the city, crossroads are commonplace because of the convenience of rectangular building plots, the density of development and more recently the ubiquitous traffic light.
In rural areas you almost never get junctions of more than four roads (unless an extra one has been sucked in by the creation of a roundabout.) Even crossroads are rare. Three-way junctions by far outnumber crossroads (I just checked this and got a ratio in the area where I am staying of about 15:1) Why would that be? Roads and paths tend to minimise distance, for fairly obvious reasons. But counter-intuitively crossroads always waste it. Here’s a drawing showing how that works:
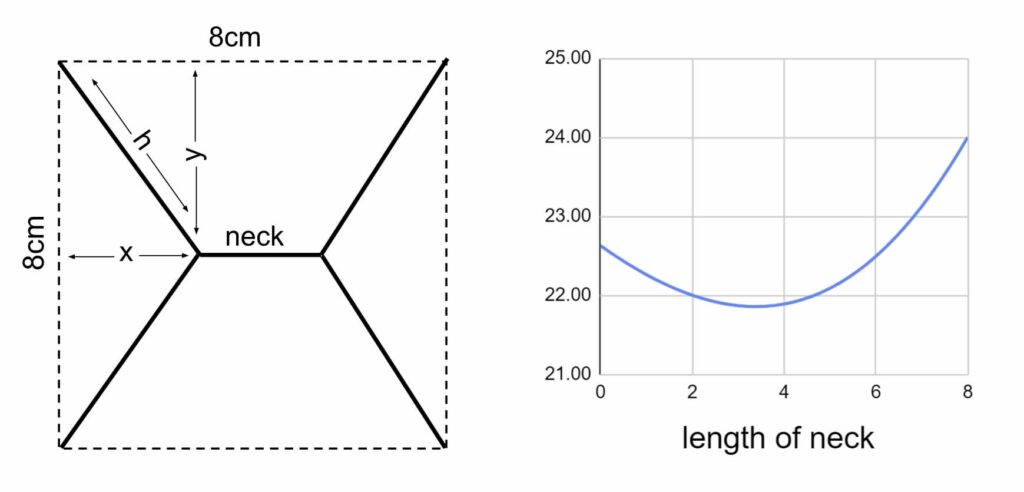
You need about 22.6cm of string to make a simple diagonal crossroads that joins the opposite corners of an 8 cm square. But add a short neck in the middle of the diagram and you can drop this total length down to about 21.8 cm. Whatever four points you are joining, it is pretty well always more economical in terms of roadbuilding to make two tee junctions rather than one crossroads.
If you have bubbles floating in water, you never get four bubbles in one plane meeting around a point. The moment you force four bubbles together in a square, two opposite ones move together forcing the other two out. The result will be three meeting at a point, never four. The same forces are pulling here; physics tries to minimise the area of the bubble film and your crossroads again becomes a pair of three-ways. Exactly the same as little roads in a rural landscape.
In three dimensions, if you press bubbles together you’ll eventually squeeze them into geometric shapes with flattish polygonal faces. Here you will get four meeting at a point. Just as in two dimensions, three lines or shapes meet to maximise economy, so in three dimensions the magic number is four. Imagine two balls next to each other on one layer, say east and west, then you want two in the next row going north and south. So four bubbles stack together in three dimensions.
Now squeeze those bubbles together, and at that junction, the bubble walls will meet in a shape which echoes those tetrahedral spicules. But that’s missing the point – it doesn’t echo them: it builds them. D’Arcy Wentworth Thompson was talking about maths and physics creating those shapes, not just describing them.
That’s a vast oversimplification. Look up pictures of spicules and they come in myriad forms that aren’t easily traced to the intersections of bubbles. But the point remains that what these ancient examples of life are doing, is this: They exploit the shapes that the laws of physics provide in the natural (without life) world. They use this to lay down material in ways that are easy or efficient or possible for them to do.
It’s one of the mysteries of the world that balls run downhill or roll off shelves. We describe a hillside as a gradient, but the law of physics that makes balls run downhill is so obvious, so universal that, so far as I know it doesn’t even have a name. But it deserves a mention, because it underlies life, and life’s nemesis – entropy. I’ll explain briefly what I’m talking about here, and come back to it later after a bit of a detour.
We call that slope a gradient and what the ball is doing is following an energy gradient. So as balls always run down a physical gradient, so things in the physical world always run down an energy gradient. This unnamed law always drives the conversion of potential energy (eg height) into kinetic energy (usually movement.) Everything in the universe so far as we know follows energy gradients in that same direction. When astrophysicists speculate about other planets, they never imagine places where things will jump up onto shelves.
Yes but isn’t that just gravity? If you look at planetary orbits without atmospheric friction or electromagnetic fields to slow things down, then this sytem is goverened by nothing but gravity and Newton’s laws. Here the arrow of time is reversible. Orbits are ellipses or parabolas. The entire trajectories of the two objects, say the earth and the moon, are calculable from their masses and velocities at any instant in their history. Both ellipses and parabolas are symmetrical, and if you were to reverse the velocity you would track their history in reverse using exactly the same equations that would predict their futures. That’s all Newton and Galileo there’s no Einstein or Bohr & Planck there. And the implication is that the arrow of time is reversible. So if it’s not gravity that determines which way energy gradients are pulling, then what is it?
Newton didn’t have coffee. As my mother would say, ‘Go easy adding that milk, you can always put a bit more, but you can’t take it out.’ She would say the same (only louder) when adding salt to stew. Newton didn’t have steam engines either. It was the analysis of these machines a couple of centuries after Newton’s time that led to the concept of entropy. Come out of orbit and down to earth and stuff doesn’t go on forever, it always slows down, producing the inevitable byproduct of unuseable heat. Those magnificent machines that turned children into slaves, and blackened the sky in rural England only returned a couple of percent of the calorific value of their fuel as power. In 1865, the lost fraction of energy was to be named entropy.
And as the concept of wasted heat developed over the next century, people realised that the new science of thermodynamics affects everything and introduces the one-way-street of time. When we add salt to a stew or milk to coffee we are following the same arrow of time that makes all heat engines inefficient. In one case the carefully exploited force of the steam is dissipated in heat and in the other the order of the salt crystal or the simple separation of milk and coffee are dissipated into the mixture. These things are all subject to the laws of thermodynamics. In the latter case the dynamics describes what is going on at molecular level and the thermo- bit means that the coffee is warm. And then it cools, sharing its energy with the room, in even more thermodynamic exchange, increasing entropy farther and so on. So entropy because associated with lukewarm chaos, the loss of organisation.
That’s all happening because when the energy gradient has done its work converting height to speed. The ball hits the bottom and it still has kinetic energy and that has to be conserved (this law does have a name.) So the ball bounces about a bit while it converts its gross kinetic energy into internal energy in the form of ricocheting molecules which we call heat.
Incidentally if you drop an ice cream and it doesn’t bounce, you might wonder whether the energy of the fall at the moment of splat has warmed it up and melted it, but the numbers don’t work like that. If all of the energy of Niagara Falls were converted to heat then the water at the bottom would be about an eighth of a centigrade degree warmer than the water in the pool at the top, (It isn’t though, because Niagara Falls faces north.) So dropping an ice cream half of one metre won’t warm anything up very much. On the other hand, if you are washing up in water that is 35 centigrade degrees hotter than room temperature, that water has extra energy equivalent of a ten mile high waterfall in your washing up bowl. No wonder that makes a difference to its ability to clean – those little bits of food are being physically knocked off the plate with a power higher than mount Everest.
But I digress. After a hundred years of thought, scientists realised that the same arrow of time that makes steam engines so inefficient, also makes it impossible to separate milk from coffee, and philosophers tore their hair out because this means that order always turns into chaos and entropy will be the death of us. And the death of the Universe. They had realised that the second law of thermodynamics describes much more than the work produced by big hot shiny steam pistons.
‘But look,’ you might say. ‘That cloud up there weighs several tons, and it’s only there because all those little water molecules defied gravity by evaporating. Not only that, but it has formed itself into the beautiful shape of a scorpion! That’s definitely order, and it came from the chaos of the ocean. Doesn’t that show that the natural forces of nature can buck entropy?’
‘No no! You don’t understand!’ wails the philosopher ‘All that only happens because the sun is shining, and when all the sun’s hydrogen runs out, then our star will fade, the scorpion will disappear and the oceans will freeze, or maybe boil. Doom! Entropy is inevitable death.’
Interesting that we should mention death there, because what the discussion of entropy doesn’t consider is life. Well maybe it does, because all life ends in death. But that’s not the point here, because the most interesting part of life happens while life is alive.
So in the natural world, even before we add life, we get planets being created and convection driving clouds uphill and thermal cells in the earth’s mantle moving tectonic plates, and mountains being made and Niagara Falls being not very good at warming water. And every one of these bits of creation is driven by energy gradients which naturally occur in the non-uniform systems left over from the Big Bang. The motor was started by gravity. Then it runs for a while following energy gradients to create motion. And finally entropy kicks in and turns it all to lukewarm chaos. Or not of course, but we haven’t got to Einsten or Hawking yet.
But meantime we have billions and billions of years for life to inhabit the interstices of the cogwheels of that great solar-powered machine of geology and climate. Little sponges are taking the gifts that the salty sea water provides and precipitating them in beautiful geometric patterns. They do this because tiny energy gradients force bubbles to minimise their potential energy by joining at tetrahedron-shaped-vertices. Here it is natural that the water will deposit calcium salts in a certain shape. So that happens.
Life exploits energy gradients, to grow. The overall forms of complex life are largely determined by evolution, but at a cellular level these spicules and shells grow because life creates systems where energy gradients running downhill create optimised structures. Then evolution forces complex systems to develop and those little energy gradient structures combine in organisms that build coral reefs, or anthills or cities.
Oops I took a jump there! But hey, we can run with that. Proteins and amino acids are complex molecules that have certain properties not (just) because of chemical reactions but because of their physical shapes. Scientists discovered that if they made two identical proteins where one is a mirror image of the other then those proteins do different things. Fast forward a few decades and AI is proposing new drug candidates by the thousand because it can predict the shape of synthetic molecules.
Inside our bodies the molecules that keep us alive are using little energy gradients all the time. We thrive and grow because our chemistry creates production lines where nutrients are converted to tissue. They do that largely because shapes fit together in a microscopic equivalent of a ball running downhill. Nature uses the energy gradients provided by physics to make structures that can adapt and reproduce. But none of this would happen and we wouldn’t be alive if stuff didn’t run downhill. Why else would our mouths be higher than our rectums?


